author: Jiaojiao Ye

tags: latent-variable model, human-robot interaction, sequential model, learning from demonstrations

Condition on a human motion, how could a robot react? We human has diverse reactive actions, but it is challenging for robots. We address this problem using Conditional VAE [3] in the human-robot interaction scenarios. CVAE is able to perform a mapping from single input to many possible outputs, and we further improve it to sequence model and predict the robot acceleration control signal.

• LSTM-based CVAE as a motion planner

We collect a data set of human-robot interactions for training and validation. Each demonstration consists of the robot end-effector positions in the cartesian space 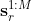, and the positions of the human hand 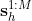, with $M$ time steps. The test data is generated online.

To implement an LSTM-based CVAE for HRI, the input of the model is 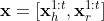and the output is the control signal $\mathbf{y} = \ddot{\mathbf{s}}_r^{t+1:t+T}$​, where $t \in [2 \dots M-T]$. $\mathbf{x}^t_h$ and $\mathbf{x}^t_r$​​​, consisting of the position, velocity, and acceleration, are the state of human and robot past trajectory from time step one to the current time step $t$​​​​​​​​ (see the notation in Fig. 1). The long output of the model from time step $t$ to $T$ is only used in the training and validation processes, resulting in more accurate predictions. However, we only use $\ddot{s}_r^{t+1}$ for testing.

Given a recognition model 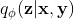, a generation model 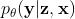, and a conditional prior model 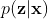, we approximates the evidence lower bound (ELBO) of the CVAE [3]:

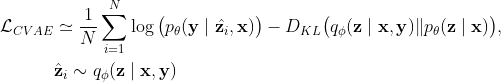
where $N$ is the number of samples. Given $\mathbf{x}$, $\mathbf{z}$ is able to model multiple modes in conditional distribution of the output $\mathbf{y}$.

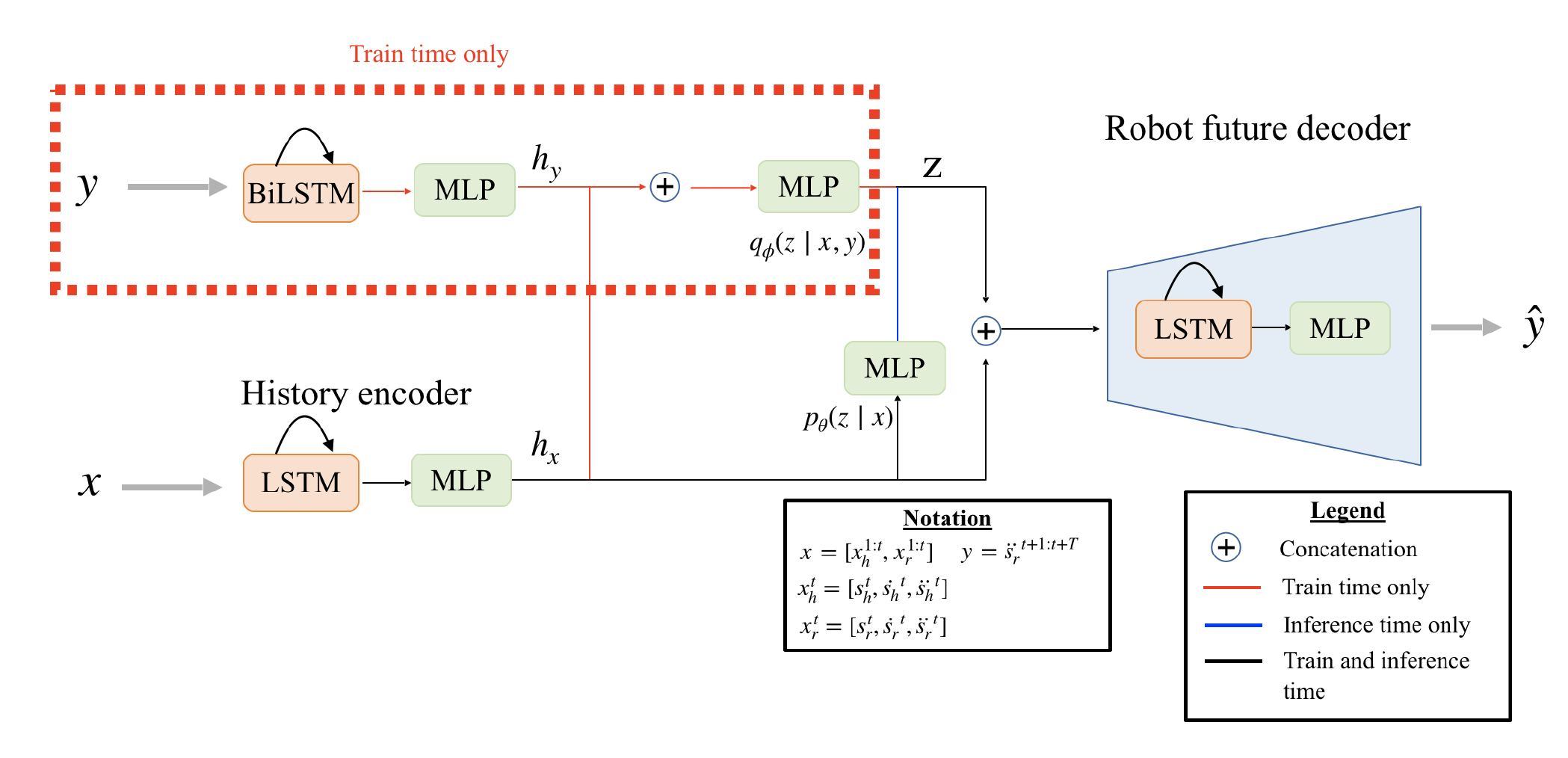Figure 1. The proposed model.

• Data augmentation for sequential data using MIXUP

Demonstration collection on a real robot is inefficient and time-consuming. Therefore, we use mixup [2] for data augmentation. In the original mixup method, discrete datapoints are augmented. Given demonstration $a$ and $b$, we adapt this technique to our specific sequential interaction dataset for both human and robot trajectories,

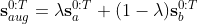
where $\lambda$ is randomly sampled.

• Best of many samples

To encourage the diversity of the generator, we employ the best of many samples [4]. It estimates the log-likelihood over the full distribution, instead of Monto-Carlo sampling,

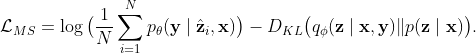
According to Jensen’s inequality, $\mathcal{L}_{BMS}$ leads to a tighter estimator to the log-likelihood

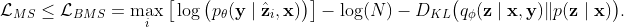
• Stable prediction

The model probably fails in motion planning due to long-term dynamics and interaction in the physical environment. We introduce a $\mathcal{L}_{Traj}$​ to regularise the velocity and position,

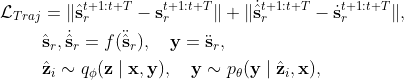
where $f$​​ represents the robot dynamic system, and $\ddot{\hat{\mathbf{s}}}_r$ is the predicted acceleration. Consequently, the model drives the robot to follow the demonstrated trajectories.

In addition, we introduce a terminal distance term to regularise the distance between the robot end-effector position and the desired target position,

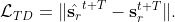
We then rewrite the loss function

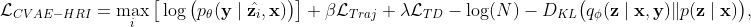
where $\beta$​​ and $\lambda$​​ are hyperparameters.

Experimental results

We illustrate our approach on a Franka Emika Panda robot arm interacting with humans. Full observations are provided by the OptiTrack motion capture system and sensors on the robot. For the training and validation datasets, the robot movements are led by a person. The goal of the robot is to reach the human hand, which is critical for e.g., handover. During testing, the robot trajectory is replanned every $1 ms$. Our model learns the correlation between humans and robots, discovers the intention of human movement, and generates the robot control signal correspondingly (see Fig. 2).

Figure 2. Robot trajectory prediction based on human movements. The upper two subfigures show the generated diverse trajectories for the robot based on similar human hand trajectories. In the lower subfigure, when human performs totally different from the demonstrations, the robot still reachs the goal.

This work was completed by Jiaojiao Ye as the master thesis in 2019-2020. The thesis is online.

Bibliography

[1] Alex Graves ,and Jurgen Schmidhuber. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks (2005).

[2] Hongyi Zhang et al. mixup: Beyond empirical risk minimization. International Conference on Learning Representations (2018).

[3] Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning Structured Output Representation using Deep Conditional Generative Models. Conference on Neural Information Processing Systems (2015).

[4] Apratim Bhattacharyya, Bernt Schiele, and Mario Fritz. Accurate and Diverse Sampling of Sequences based on a “Best of Many” Sample Objective. IEEE Conference on Computer Vision and Pattern Recognition (2018).